March 15, 2025
Structured hashing with deep learning for modality, organ, and disease content sensitive medical image retrieval
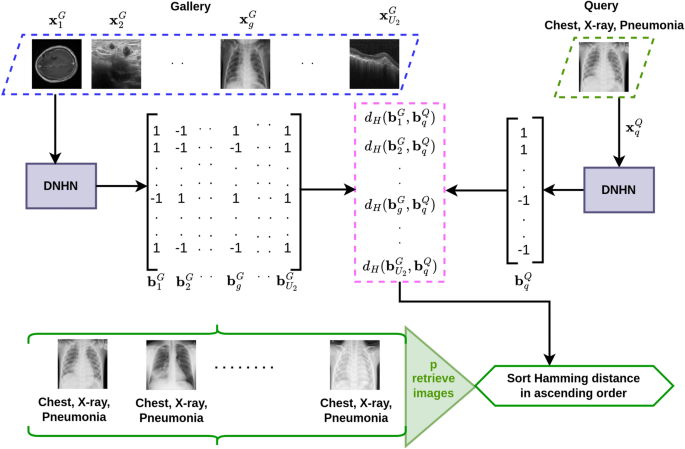
Problem formulation Consider a training set \(\textbf{X}_{\mathfrak {T}} = \{\textbf{x}_{1}^{\mathfrak {T}}, \textbf{x}_2^{\mathfrak {T}}, \dots , \textbf{x}_i^{\mathfrak {T}}, \dots , \textbf{x}_{U_1}^{\mathfrak {T}} \}\). Let, \(\textbf{y}_i^{\mathfrak {T}}= [\textbf{y}_{1i}^{\mathfrak {T}}, \textbf{y}_{2i}^{\mathfrak {T}}, \textbf{y}_{3i}^{\mathfrak {T}}]\) represents the label of image \(\textbf{x}_i^{\mathfrak {T}} \in \mathbb {R} ^{1 \times M \times N}\). \(\textbf{y}_{1i}^{\mathfrak {T}} \in \{0,1\}^{\lambda \times 1}, \textbf{y}_{2i}^{\mathfrak {T}} \in \{0,1\}^{\mu \times 1},\) and \(\textbf{y}_{3i}^{\mathfrak {T}} \in \{0,1\}^{\nu \times 1}\) are the respective labels (one hot vector) of modality, organ and disease corresponding the image \(\textbf{x}_i^{\mathfrak {T}}\). \(\lambda\), \(\mu\), and \(\nu\) are the number of modalities, organs and diseases in the training set respectively. The